题目内容
18.已知二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),(5,0),图象上有三个点(x1,y1),(x2,y2),(x3,y3).若当x1<-1<x2<5<x3时,均有y1y2<0,y2y3<0,则下列说法中正确的是( )| A. | a<0 | B. | x=2时,y有最大值 | C. | y1y2y3<0 | D. | 5b=4c |
分析 根据抛物线的性质即可判定A、B、C错误,由交点坐标,求得对称轴,得出a和b的关系,根据x=-1时,y=0,得出a-b+c=0,根据a、b的关系即可求得5b=4c.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),(5,0),
∴对称轴为x=$\frac{-1+5}{2}$=2,
∵当x1<-1<x2<5<x3时,均有y1y2<0,y2y3<0,
∴当a>0,y有最小值,y1,>0,y2<0,y3>0,当a<0,y有最大值,y1,<0,y2>0,y3<0,
∴y1y2y3>0,
故A、B、C错误,
∵-$\frac{b}{2a}$=2,
∴a=-$\frac{1}{4}$b,
∵图象经过点(-1,0),
∴a-b+c=0,
∵-$\frac{1}{4}$b-b+c=0,
∴5b=4c,故D正确;
故选D.
点评 本题考查了二次函数的性质,根据交点坐标求得对称轴是解题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
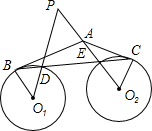 如图,AB切⊙O1于点B,AC切⊙O2于点C,BC分别交⊙O1、⊙O2于点D、E,延长O1D、O2E交于点P.若∠BAC=130°,∠ABC=20°,则∠P的度数为( )
如图,AB切⊙O1于点B,AC切⊙O2于点C,BC分别交⊙O1、⊙O2于点D、E,延长O1D、O2E交于点P.若∠BAC=130°,∠ABC=20°,则∠P的度数为( )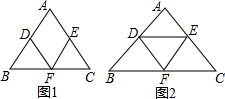 已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.
已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.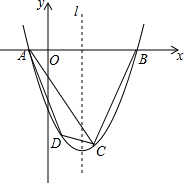 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.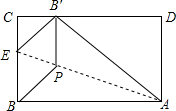 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.