题目内容
11.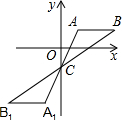 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n-1) | D. | (-m,-n+1) |
分析 设点A的坐标为(x,y),然后根据中心对称的点的特征列方程求解即可.
解答 解:设点A的坐标为(x,y),
∵△ABC绕点C(0,-1)旋转180°得到△A1B1C1,点A1的坐标为(m,n),
∴$\frac{x+m}{2}$=0,$\frac{y+n}{2}$=-1,
解得x=-m,y=-n-2,
所以,点A的坐标为(-m,-n-2).
故选B.
点评 本题考查了坐标与图形变化-旋转,熟练掌握中心对称的点的坐标特征是解题的关键.

练习册系列答案
相关题目
19.(-$\frac{1}{2}$)0的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | -$\frac{1}{2}$ |
20.下列命题中,真命题是( )
| A. | 连接矩形各边中点的四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 三个角相等的四边形是矩形 | D. | 两条对角线相等的四边形是矩形 |
1.按一定的规律排列的两行数:
猜想并用关于n的代数式表示m=m=$\frac{1}{2}$(n2-1).
| n(n是奇数,且n≥3) | 3 | 5 | 7 | 9 | … |
| m(m是偶数,且m≥4) | 4 | 12 | 24 | 40 | … |
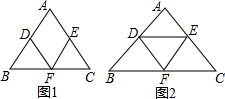 已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.
已知,△ABC中,AB=AC,点D,E,F分别是边AB,AC,BC的中点,连接DF与EF.
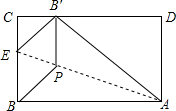 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.