题目内容
9.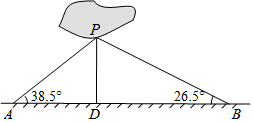 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)(参考数据:sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80,sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50)
分析 设PD=x米,在Rt△PAD中表示出AD,在Rt△PDB中表示出BD,再由AB=200.0米,可得出方程,解出即可得出PD的长度,继而也可确定小桥在小道上的位置.
解答 解:设PD=x米,
∵PD⊥AB,
∴∠ADP=∠BDP=90°,
在Rt△PAD中,tan∠PAD=$\frac{x}{AD}$,
∴AD=$\frac{x}{tan38.5°}$≈$\frac{x}{0.8}$=$\frac{5}{4}$x,
在Rt△PBD中,tan∠PBD=$\frac{x}{BD}$,
∴DB=$\frac{x}{tan26.5°}$≈$\frac{x}{0.50}$=2x,
又∵AB=80.0米,
∴$\frac{5}{4}$x+2x=200.0,
解得:x≈61.5,即PD≈61.5(米),
∴DB=123.0(米).
答:小桥PD的长度约为61.5米,位于AB之间距B点约123.0米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.

练习册系列答案
相关题目
 如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$.
如图,在△ABC中,BC=AC=4,∠C=90°,在平面内,△ABC绕点A逆时针旋转α,对应得△AB′C′,以B′C′为直径的圆第一次与直线AB相切时.若B′C′中点为O,过O作OH⊥AB交AB′于点G,则S△B′OG=$\frac{8}{7}$. 如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方.
如图,我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域,在航线AB同一水平面上,有三座岛屿C、D、E.船在A处时,测得岛C在A处南偏东15°方向距离A处$\sqrt{2}$a(a>0)海里,岛D在A处南偏东60°方向距离A处a海里,岛E在A处东南方向,当船航行到达B处时,此时测得岛E恰好在船的正南方. 为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.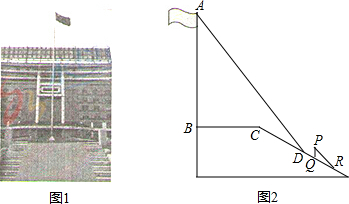
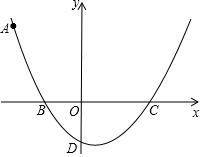 如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).
如图,在平面直角坐标系内,点O为坐标原点,经过点A(-4,4)的抛物线y=$\frac{1}{k}$(x+2)(x+a)交x轴负半轴于点B,交x轴正半轴于点C,交y轴于点D(0,-2).