题目内容
19.梯形ABCD中,AB∥CD,对角线AC与BD相交于O.若S△ABO=p,S△CDO=q,求SABCD.分析 由平行线得出△AOD∽△COB,得出面积比等于相似比的平方,求出OA:OC,得出△DOC的面积和△AOB的面积,即可得出梯形ABCD的面积.
解答 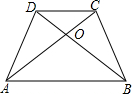 解:∵AB∥CD,
解:∵AB∥CD,
∴△COD∽△AOB,
∴$\frac{{S}_{△COD}}{{S}_{△AOB}}$=$\frac{p}{q}$,
∴$\frac{OD}{OB}$=$\frac{\sqrt{p}}{\sqrt{q}}$,
∵$\frac{{S}_{△AOD}}{{S}_{△AOB}}$=$\frac{OD}{OB}$=$\frac{\sqrt{p}}{\sqrt{q}}$,
∴S△AOD=$\frac{1}{\sqrt{pq}}$=$\frac{\sqrt{pq}}{pq}$,
∴S△BOC=S△AOD=$\frac{\sqrt{pq}}{pq}$,
∴梯形ABCD的面积=S△DOC+S△AOB+S△COB+S△AOD=q+p+$\frac{\sqrt{pq}}{pq}$+$\frac{\sqrt{pq}}{pq}$=p+q+$\frac{2\sqrt{pq}}{pq}$.
点评 本题考查了梯形的性质、相似三角形的判定与性质、三角形的面积关系;熟练掌握梯形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
 如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠AOB=135°,则∠ACB的度数为( )| A. | 35° | B. | 55° | C. | 60° | D. | 67.5° |
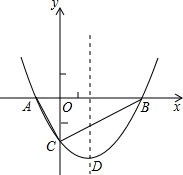 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
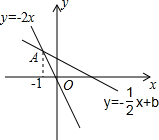 如图,在平面直角坐标系中直线y=-2x与y=-$\frac{1}{2}$x+b交于点A,则关于x,y的方程组$\left\{\begin{array}{l}{x+2y=2b}\\{2x+y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.
如图,在平面直角坐标系中直线y=-2x与y=-$\frac{1}{2}$x+b交于点A,则关于x,y的方程组$\left\{\begin{array}{l}{x+2y=2b}\\{2x+y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$. 实数a、b在数轴上对应点的位置如图所示,则a<b(填“<”、“>”或“=”).
实数a、b在数轴上对应点的位置如图所示,则a<b(填“<”、“>”或“=”).