题目内容
5. 如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )
如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
分析 根据圆周角定理得到∠ACB=90°,根据等腰直角三角形的性质求出∠A的度数,根据圆周角定理得到答案.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CA=CB,
∴∠A=∠ABC=45°,
∴∠D=∠A=45°,
故选:C.
点评 本题考查的是圆周角定理和等腰直角三角形的性质,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
16.两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:16 |
17.下列计算正确的是( )
| A. | -(-2)2=22 | B. | (-3)2=6 | C. | -24=(-2)4 | D. | (-2)3=-23 |
14.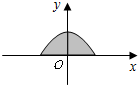 如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
 如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )
如图所示是二次函数y=-$\frac{1}{2}$x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为与其最接近的值是( )| A. | 4 | B. | $\frac{16}{3}$ | C. | 2π | D. | 8 |
 实数a、b在数轴上对应点的位置如图所示,则a<b(填“<”、“>”或“=”).
实数a、b在数轴上对应点的位置如图所示,则a<b(填“<”、“>”或“=”).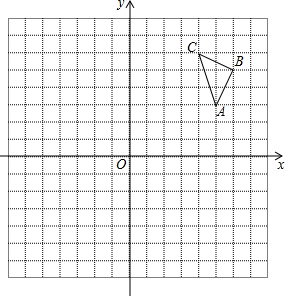 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).