题目内容
14.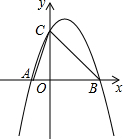 已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:
已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:(1)S△AOC=$\frac{3}{2}$;
(2)S△BOC=$\frac{9}{2}$;
(3)S△ABC=6;
(4)S△COP=$\frac{3}{2}$;
(5)S△PAB=8;
(6)S△PCB=3;
(7)S△ACP=1;
(8)若D为抛物线上的一动点(点D与点C不重合),且S△ABD=S△ABC,求点D的坐标.
分析 根据抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,可以分别求得点A、B、C、P的坐标,从而可以求得各三角形的面积,第(8)问中两个三角形面积相等,可知两个三角形以AB为底边,高相等,从而可以求得点D的坐标.
解答 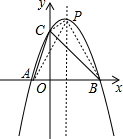 解:将y=0代入y=-x2+2x+3,得-x2+2x+3=0,
解:将y=0代入y=-x2+2x+3,得-x2+2x+3=0,
解得,x=-1或x=3,
即点A的坐标为(-1,0),点B的坐标为(3,0),
将x=0代入y=-x2+2x+3,得y=3,
即点C的坐标为(0,3),
∵y=-x2+2x+3=-(x-1)2+4,
∴点P的坐标为(1,4),
∴(1)${S}_{△AOC}=\frac{AO•OC}{2}=\frac{1×3}{2}=\frac{3}{2}$,
(2)${S}_{△BOC}=\frac{BO•OC}{2}=\frac{3×3}{2}=\frac{9}{2}$,
(3)${S}_{△ABC}=\frac{AB•OC}{2}=\frac{4×3}{2}=6$,
(4)${S}_{△COP}=\frac{3×1}{2}=\frac{3}{2}$,
(5)${S}_{△PAB}=\frac{4×4}{2}=8$,
(6)${S}_{△PCB}=\frac{(3+4)×1}{2}+\frac{2×4}{2}-\frac{3×3}{2}$=3,
(7)${S}_{△ACP}=\frac{1×3}{2}+\frac{(3+4)×1}{2}-\frac{2×4}{2}$=1,
故答案为:$\frac{3}{2},\frac{9}{2},6,\frac{3}{2},8,3,1$.
(8)∵S△ABD=S△ABC,D为抛物线上的一动点(点D与点C不重合),
∴将y=3代入y=-x2+2x+3,得x=2或x=0(舍去),
将y=-3代入y=-x2+2x+3,得$x=1+\sqrt{7}$或x=1-$\sqrt{7}$,
即点D的坐标为(2,3)或($1+\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3).
点评 本题考查抛物线与x轴的交点,解题的关键是明确题意,找出所求问题需要的条件.

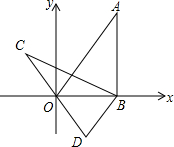 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).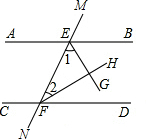 如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?
如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?