题目内容
4.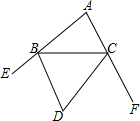 已知,如图,BD,CD分别为∠EBC和∠FCB的平分线.
已知,如图,BD,CD分别为∠EBC和∠FCB的平分线.(1)若∠A=80°,且∠D的度数;
(2)试探究∠D和∠A的关系.
分析 (1)先根据角平分线的定义得出∠CBD=$\frac{1}{2}$∠CBE,∠BCD=$\frac{1}{2}$∠BCF,再根据三角形外角的性质得出∠D=180°-(∠CBD+∠BCD)=90°-$\frac{1}{2}$∠A,把∠A=80°代入即可得出结论;
(2)根据(1)中的证明过程即可得出结论.
解答 解:(1)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=$\frac{1}{2}$∠CBE,∠BCD=$\frac{1}{2}$∠BCF,
∴∠CBD+∠BCD
=$\frac{1}{2}$∠CBE+$\frac{1}{2}$∠BCF
=$\frac{1}{2}$(∠CBE+∠BCF)
=$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=$\frac{1}{2}$(180°+∠A),
∴∠D=180°-(∠CBD+∠BCD)
=180°-$\frac{1}{2}$(180°+∠A)
=90°-$\frac{1}{2}$∠A
=90°-$\frac{1}{2}$×80°
=50°.
(2)∵BD、CD分别是∠EBC和∠FCB的平分线,
∴∠CBD=$\frac{1}{2}$∠CBE,∠BCD=$\frac{1}{2}$∠BCF,
∴∠CBD+∠BCD
=$\frac{1}{2}$∠CBE+$\frac{1}{2}$∠BCF
=$\frac{1}{2}$(∠CBE+∠BCF)
=$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=$\frac{1}{2}$(180°+∠A),
∴∠D=180°-(∠CBD+∠BCD)
=180°-$\frac{1}{2}$(180°+∠A)
=90°-$\frac{1}{2}$∠A.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

| A. | 41 | B. | 47 | C. | 50 | D. | 58 |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
 在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.
在4×4的方格中有五个同样大小的正方形按图示位置摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有( )个.