题目内容
15. 如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )
如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )| A. | 32cm | B. | 31cm | C. | 9cm | D. | 18cm |
分析 先连接OA,过点O作OC⊥AB,交⊙O于D,根据垂径定理,即可求得AC的值,然后在Rt△OAC中,利用勾股定理,即可求得OC的值,继而求得油的最大深度.
解答 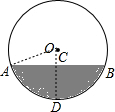 解:如图,过O作OC⊥AB于点C,并延长交⊙O于点D,连结OA,
解:如图,过O作OC⊥AB于点C,并延长交⊙O于点D,连结OA,
依题意得CD就是油的最大深度,
根据垂径定理得:AC=$\frac{1}{2}$AB=40cm,OA=41cm,
在Rt△OAC中,根据勾股定理得:OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{4{1}^{2}-4{0}^{2}}$=9(cm),
∴CD=OD-OC=41-9=32(cm),
故选A.
点评 此题考查了垂径定理的应用.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4. 如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )
如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )
 如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )
如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是( )| A. | 两点之间,线段最短 | B. | 射线只有一个端点 | ||
| C. | 两直线相交只有一个交点 | D. | 两点确定一条直线 |
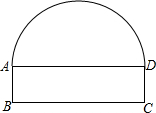 如图,隧道的截面由半圆和长方形构成,长方形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?
如图,隧道的截面由半圆和长方形构成,长方形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?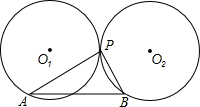 已知:如图,两个半径长为r的等圆⊙O1和⊙O2外切于点P,A是⊙O1上的一点,BP⊥AP,BP交⊙O2于点B.求证:AB=2r.
已知:如图,两个半径长为r的等圆⊙O1和⊙O2外切于点P,A是⊙O1上的一点,BP⊥AP,BP交⊙O2于点B.求证:AB=2r. 已知函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,化简:|m-3|-$\sqrt{{n}^{2}-4n+4}$.
已知函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,化简:|m-3|-$\sqrt{{n}^{2}-4n+4}$.