题目内容
17.若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是1:2.分析 根据相似三角形面积的比等于相似比的平方求出相似比,根据似三角形周长的比等于相似比得到答案.
解答 解:∵两个相似三角形的面积比为1:4,
∴这两个相似三角形的相似比为1:2,
∴这两个相似三角形的周长比是1:2,
故答案为:1:2.
点评 本题考查的是相似三角形的性质,掌握相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.计算3a2-a2的结果是( )
| A. | 4a2 | B. | 3a2 | C. | 2a2 | D. | 3 |
12. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | 2π | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
9.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2b)3=-6a6b3 | C. | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D. | (a+b)2=a2+b2 |
15. 如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )
如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )
 如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )
如图,在直径为82cm的圆柱形油槽内装有一些油以后,油面宽AB=80cm,则油的最大深度为( )| A. | 32cm | B. | 31cm | C. | 9cm | D. | 18cm |
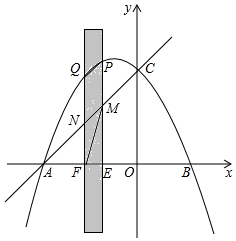 如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
如图,抛物线与x轴交于点A(-5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.