题目内容
6.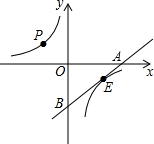 如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )
如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )| A. | 24 | B. | 12 | C. | 6 | D. | 不确定 |
分析 先利用待定系数法求出双曲线的解析式为y=-$\frac{6}{x}$,再设直线AB的解析式为y=kx+b,联立直线与双曲线的解析式得出关于x的一元二次方程,根据△=0得出b2=24k,把b2=24k代入△AOB面积的表达式即可求解.
解答 解:∵点P(-2,3)在双曲线上,
∴双曲线的解析式为y=-$\frac{6}{x}$.
设直线AB的解析式为y=kx+b.
联立$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{6}{x}}\end{array}\right.$,得 kx2+bx+6=0,
∵直线与双曲线只有一个公共点,
∴△=b2-4•k•6=0,即b2=24k.
∵直线y=kx+b与x轴和y轴分别交于A、B两点,
∴A(-$\frac{b}{k}$,),B(0,b),
∴△AOB面积=$\frac{1}{2}$•|-$\frac{b}{k}$|•|b|=$\frac{{b}^{2}}{2k}$=$\frac{24k}{2k}$=12.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题,利用待定系数法求双曲线的解析式,一元二次方程根的判别式,三角形的面积,由直线AB与双曲线只有一个公共点得出b2=24k是解题的关键.

练习册系列答案
相关题目
11.不等式x-2≤0的解集在以下数轴表示中正确的是( )
| A. |  | B. | 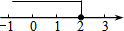 | C. | 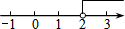 | D. | 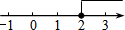 |
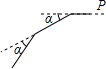 寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.
寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.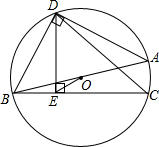 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.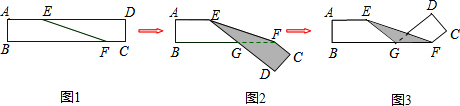
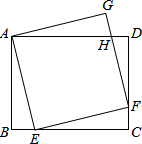 如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.
如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.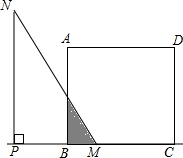 如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.
如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.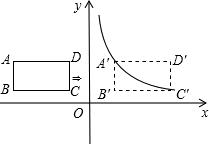 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.