题目内容
9.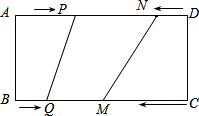 如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
分析 首先利用x表示出PN和QM的长,然后根据PN=QM即可列方程求得x的值.
解答 解:由题意知,点Q只能在点M的左侧,
①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),
整理得x2-2x=0,
解这个方程,得x1=0(舍去),x2=2.
所以,当x=2时,四边形PQMN是平行四边形.
②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-2,
整理得x2+6x-40=0,
解这个方程,得x1=-10(舍去),x2=4.
所以,当x=4时,四边形NQMP是平行四边形.
所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.
点评 本题考查了平行四边形的判定,有一组对边相等且平行的四边形是平行四边形,正确进行讨论是关键.

练习册系列答案
相关题目
4.用配方法解方程x2+4x+1=0,则配方正确的是( )
| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+2)2=-3 | D. | (x+4)2=3 |
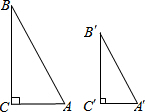 学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.
学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.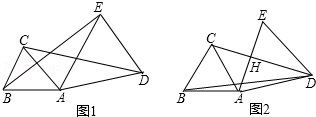
 已知:点D在AB上,点E在AC上,BE⊥AC,CD⊥AB,AB=AC,求证:∠B=∠C.
已知:点D在AB上,点E在AC上,BE⊥AC,CD⊥AB,AB=AC,求证:∠B=∠C. .
.
 圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?
圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?