题目内容
14．
已知：点D在AB上，点E在AC上，BE⊥AC，CD⊥AB，AB=AC，求证：∠B=∠C．
分析 根据AAS证明△ABE与△ACD全等，再利用全等三角形的性质证明即可．
解答 证明：∵BE⊥AC，CD⊥AB，
∴∠AEB=∠ADC=90°，
在△ABE与△ACD中，
$\left\{\begin{array}{l}{∠AEB=∠ADC=90°}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$，
∴△ABE≌△ACD（AAS），
∴∠B=∠C．
点评 本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．
练习册系列答案
相关题目
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，则∠1的度数是75°．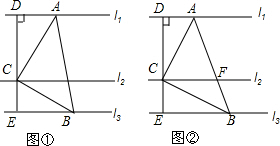
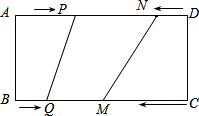如图，在矩形ABCD中，BC=20cm，P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在矩形的边上同时运动，当有一个点到达所在运动的另一个端点时，运动即停止．已知在相同时间内，若BQ=xcm（x＞0），则AP=2xcm，CM=3xcm，DN=x2cm．当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形．
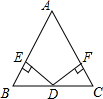如图，已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
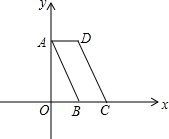如图，点O为平面直角坐标系的原点，在?ABCD中，A（0，4），B（2，0），C（4，0），过A作直线AE交x轴FE点，tan∠AEO=$\frac{4}{3}$ 
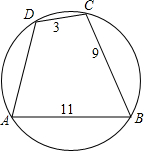已知圆内接四边形ABCD中，AB=11，BC=9，CD=3，如图，$\widehat{AB}$+$\widehat{CD}$=$\widehat{BC}$+$\widehat{AD}$，则AD=7．