题目内容
17.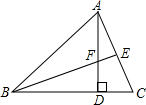 如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,则
如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,则BE=$\frac{48}{5}$.
分析 利用三角形面积公式得到$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AC•BE,然后利用比例性质可求出BE.
解答 解:∵AD⊥BC于D,AD=5,BE⊥AC于E,
∴S△ABC=$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AC•BE,
∴BE=$\frac{BC•AD}{AC}$=$\frac{8×6}{5}$=$\frac{48}{5}$.
故答案为$\frac{48}{5}$.
点评 本题考查了三角形的面积:记住三角形面积公式,三角形的面积等于底边长与高线乘积的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.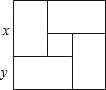 用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
 用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )| A. | x+y=14 | B. | x-y=2 | C. | xy=48 | D. | x2+y2=144 |
7.抛物线y=-2(x+6)2+5的顶点坐标是( )
| A. | (-6,5) | B. | (6,5) | C. | (6,-5) | D. | (-2,5) |
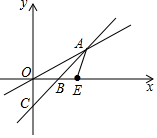 如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.
如图,直线y=x-m与直线y=kx(k≠0)交于点A,直线y=x-m与x轴交于点B,与y轴交于点C,若直线y=kx(k≠0)与x轴正半轴所成夹角为30°,OB=$2({\sqrt{3}-1})$.
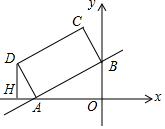 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.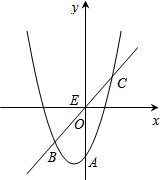 顶点为(-$\frac{1}{2}$,-$\frac{17}{4}$)的抛物线与y轴交于点A(0,-4),E(0,b)(b>-4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点.
顶点为(-$\frac{1}{2}$,-$\frac{17}{4}$)的抛物线与y轴交于点A(0,-4),E(0,b)(b>-4)为y轴上一动点,过点E的直线y=x+b与抛物线交于B、C两点.