题目内容
2.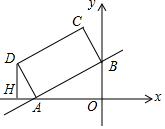 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.(1)求边AB的长;
(2)求点D的坐标.
分析 (1)根据直线解析式求出OA、OB,再利用勾股定理列式计算即可得解;
(2)根据矩形的性质可得∠BAD=90°,然后求出∠BAO=∠ADH,再求出△AOB和△DHA相似,根据相似三角形对应边成比例求出AH、DH,再求出OH,然后根据点D在第二象限写出即可.
解答 解:(1)令y=0,则$\frac{1}{2}$x+2=0,
解得x=-4,
令x=0,则y=2,
所以OA=4,OB=2,
根据勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
(2)∵矩形ABCD,
∴∠BAD=90°,
∴∠DAH+∠BAO=90°,
∵DH⊥x轴,
∴∠AHD=90°,
∴∠DAH+∠ADH=90°,
∴∠BAO=∠ADH,
又∵∠AHD=∠BOA=90°,
∴△AOB∽△DHA,
∴$\frac{DH}{OA}$=$\frac{AH}{OB}$=$\frac{AD}{AB}$,
即$\frac{DH}{4}$=$\frac{AH}{2}$=$\frac{\sqrt{5}}{2\sqrt{5}}$,
解得DH=2,AH=1,
所以,OH=OA+AH=4+1=5,
所以,点D的坐标为(-5,2).
点评 本题考查了一次函数图象上点的坐标特征,勾股定理,矩形的性质,相似三角形的判定与性质,熟记定理与性质并确定出相似三角形是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 将一副三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是72cm2.
将一副三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是72cm2.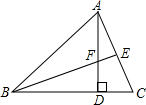 如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,则
如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,则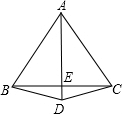 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm.
如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm.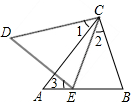 如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.
如图,点E在AB上,∠CEB=∠B,∠1=∠2=∠3,求证:CD=CA.