题目内容
18.抛物线y=x2-2x+m与x轴交于A,B两点,顶点为C.(1)求m的取值范围;
(2)若△ABC是直角三角形,求m的值.
分析 (1)由题意得出方程x2-2x+m=0有两个不相等的实数根,得出b2-4ac=0,即(-2)2-4×1×m>0,解不等式即可;
(2)由题意得出△ABC是等腰三角形,若△ABC是直角三角形,则CD=$\frac{1}{2}$AB,AB=b-a,由根与系数的关系得出a+b=2,ab=m,得出关于m的方程,解方程即可.
解答 解:(1)∵抛物线y=x2-2x+m与x轴交于A,B两点,
∴方程x2-2x+m=0有两个不相等的实数根,
∴b2-4ac>0,
即(-2)2-4×1×m>0,
∴m<1;
(2)∵抛物线y=x2-2x+m与x轴交于A,B两点,顶点为C,
∴△ABC是等腰三角形,
若△ABC是直角三角形,设抛物线与x轴的交点为D,点A、B的横坐标分别为a、b(a<b),
则CD=$\frac{1}{2}$AB,AB=b-a,
由根与系数的关系得:a+b=2,ab=m,
∵抛物线y=x2-2x+m=(x-1)2+m-1,
∴C(2,m-1),
∴CD=|m-1|=1-m,
∴1-m=$\frac{1}{2}$(b-a)=$\frac{1}{2}$$\sqrt{(a+b)^{2}-4ab}$=$\sqrt{{2}^{2}-4m}$,
解得:m=0,或m=1(舍去),
∴m=0.
点评 本题考查了抛物线与x轴的交点、根的判别式、根与系数的关系、不等式的解法、直角三角形斜边上的中线性质、一元二次方程的解法等知识;由根与系数的关系和直角三角形斜边上的中线性质得出方程是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
10.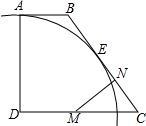 如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
 如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )
如图,四边形ABCD中∠D=90°,以点D为圆心,AD为半径作⊙D,AB和BC分别切⊙D于点A和点E,若AB=4,DC=10,点M、N分别在线段DC、BC上,且MN=DM,则DM的最小值为( )| A. | 5 | B. | 6 | C. | 5.5 | D. | $\frac{40}{9}$ |
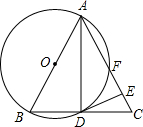 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E. 如图,AB是⊙O的直径,CB切⊙O于B.过点A作OC的平行线,交⊙O于D,那么CD是⊙O的切线吗?证明你的结论.
如图,AB是⊙O的直径,CB切⊙O于B.过点A作OC的平行线,交⊙O于D,那么CD是⊙O的切线吗?证明你的结论.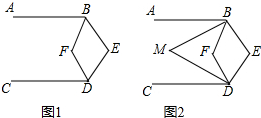
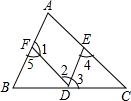 已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.
已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.