Question

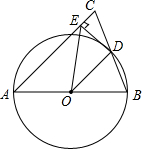
6．如图，AB是⊙O的直径，CB切⊙O于B．过点A作OC的平行线，交⊙O于D，那么CD是⊙O的切线吗？证明你的结论．

Answer 1

分析 连接OD，由DA与CO平行，利用两直线平行内错角相等、同位角相等得到两对角相等，再由OD=OA，利用等边对等角得到一对角相等，等量代换得到∠COB=∠COD，再由OD=OB，OC为公共边，利用SAS得出三角形BCO与三角形DCO全等，由全等三角形对应角相等得到一对角相等，由BC为圆的切线，利用切线的性质得到∠CBO=90°，进而得到∠CDO=90°，再由OD为圆的半径，即可得到CD为圆O的切线．

解答 证明：连接OD，
∵AD∥OC，
∴∠COB=∠DAO，∠COD=∠ADO，
∵OD=OA，
∴∠DEO=∠EDO，
∴∠COB=∠COD，
在△BCO和△DCO中，
$\left\{\begin{array}{l}{OB=OD}\\{∠COB=∠COD}\\{OC=OC}\end{array}\right.$，
∴△BCO≌△DCO（SAS），
∴∠CDO=∠CBO，
∵BC为圆O的切线，
∴BC⊥OB，即∠CBO=90°，
∴∠CDO=90°，
又∵OD为圆的半径，
∴CD为圆O的切线．

点评 此题考查了切线的判定与性质，以及全等三角形的判定与性质，熟练掌握切线的判定方法是解本题的关键．