题目内容
3．如果抛物线y=x2-x+k（k为常数）与x轴只有一个公共点，那么k=$\frac{1}{4}$．分析 令y=0，则关于x的一元二次方程x2-x+k=0的根的判别式△=0，据此列出关于k的新方程，通过解新方程即可求得k的值．
解答 解：令y=0，则当抛物线y=x2-x+k与x轴只有一个公共点时，
关于x的一元二次方程x2-x+k=0的根的判别式△=0，即（-1）2-4×1×k=0，
解得：k=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．
点评 本题考查了抛物线与x轴的交点．解题时，运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系：当b2-4ac=0时，只有一个交点”求解即可．
练习册系列答案
相关题目
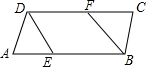完成下面证明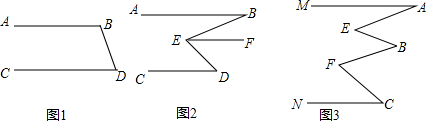
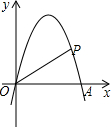如图，在平面直角坐标系中，抛物线y=-x2+4x与x轴交于点O、A，点P在抛物线上，连结OP、AP，设点P的横坐标为m，△AOP的面积为S，若0＜m＜3，则S的取值范围是0＜S≤8．
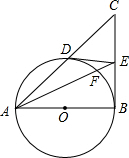如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于D，过点D作⊙O的切线交BC于E，AE交⊙O于点F．