题目内容
3.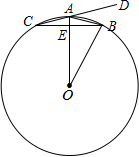 如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+∠AOB=60°
(1)求∠AOB的度数;
(2)若AE=1,求BC的长.
分析 (1)连接OC,根据垂径定理和三角形的外角的性质证明∠DAB=∠AOB,求出∠AOB的度数;
(2)根据直角三角形的性质得到BE=$\frac{1}{2}$OB,设⊙O的半径为r,根据勾股定理求出r,根据等边三角形的性质得到答案.
解答 解:(1)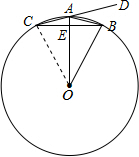 连接OC,
连接OC,
∵OA⊥BC,OC=OB,
∴∠AOC=∠AOB,∠ACO=∠ABO,
∵∠DAO=∠ACO+∠AOC=∠OAB+∠DAB,∠ACO=∠OAB,
∴∠DAB=∠AOC,
∴∠DAB=∠AOB,又∠DAB+∠AOB=60°,
∴∠AOB=30°;
(2)∵∠AOB=30°,
∴BE=$\frac{1}{2}$OB,
设⊙O的半径为r,则BE=$\frac{1}{2}$r,OE=r-1,
由勾股定理得,r2=($\frac{1}{2}$r)2+(r-1)2,
解得r1=4+2$\sqrt{3}$,r2=4-2$\sqrt{3}$(舍去)
∵OB=OC,∠BOC=2∠AOB=60°,
∴BC=r=4+2$\sqrt{3}$.
点评 本题考查的是勾股定理、圆周角定理和垂径定理的应用,正确作出辅助线、理解垂直于弦的直径平分这条弦、等边对等角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列式子,符合代数式书写格式的是( )
| A. | a+b人 | B. | 1$\frac{1}{3}$a | C. | a×8 | D. | $\frac{b}{a}$ |
15.一元二次方程x(x+2)=x的根为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 0或-2 |
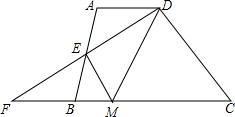 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.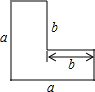 如图“L”形的图形的面积有如下四种表示方法:
如图“L”形的图形的面积有如下四种表示方法: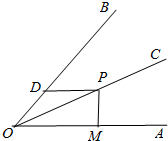 如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )
如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )