题目内容
14.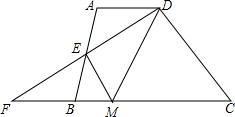 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点M在BC边上,且∠MDF=∠ADF.(1)求证:△ADE≌△BFE.
(2)如果FM=CM,求证:EM垂直平分DF.
分析 (1)根据AD∥BC,可得∠A=∠EBF,∠ADE=∠F,由E是AB的中点,可得AB=BE,从而可以证明△ADE≌△BFE;
(2)由△ADE≌△BFE,可得DE与EF相等,点E为DF的中点,再根据∠MDF=∠ADF,AD∥BC,FM=CM,可以得到MF=MD,然后根据等腰三角形三线合一,可以证明结论成立.
解答 证明:(1)∵AD∥BC,
∴∠A=∠EBF,∠ADE=∠F.
∵E是AB的中点,
∴AE=BE.
在△ADE与△BFE中,
$\left\{\begin{array}{l}{∠A=∠EBF}\\{∠ADE=∠F}\\{AE=BE}\end{array}\right.$,
∴△ADE≌△BFE(AAS).
(2)∵AD∥BC,
∴∠ADE=∠F.
∵∠MDF=∠ADF,
∴∠MDF=∠F.
∴FM=DM.
∵△ADE≌△BFE,
∴EF=DE.
∴点E为边DF的中点.
∴ME⊥DF.
即EM垂直平分DF.
点评 本题考查三角形的全等、平行线的性质、等腰三角形的性质,解题的关键是正确分析题意,找出所求问题需要的条件.

练习册系列答案
相关题目
19.若点A(2,m)在x轴上,则点B(m-1,m+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.下列说法中正确的是( )
| A. | 单项式$\frac{-2{x}^{2}y}{5}$的系数是-2,次数是3 | |
| B. | -a是单项式,表示负数 | |
| C. | -6x2y+4x-1是二次三项式 | |
| D. | 单项式-$\frac{{3}^{2}ab}{2}$的次数是2,系数是-$\frac{9}{2}$ |
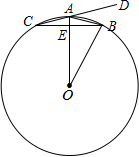 如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+