题目内容
18.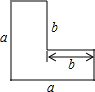 如图“L”形的图形的面积有如下四种表示方法:
如图“L”形的图形的面积有如下四种表示方法:①a2-b2;②a(a-b)+b(a-b);③(a+b)(a-b); ④(a-b)2.
其中正确的表示方法有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 利用不同的分割方法把:原图形剪成两部分,它们分别是边长为a、a-b和b、a-b的矩形;沿对角线将原图分成两个直角梯形,将它们的对角线重合,拼成一个新的矩形;把原图形看作边长为a和边长为b的正方形的面积差.由此分别求得答案即可.
解答 解:如图①,
图①中,大正方形面积为a2,小正方形面积为b2,所以整个图形的面积为a2-b2;
如图②,
一个矩形的面积是b(a-b),另一个矩形的面积是a(a-b),所以整个图形的面积为a(a-b)+b(a-b);
如图③,
在图③中,拼成一长方形,长为a+b,宽为a-b,则面积为(a+b)(a-b).
综上所知:矩形的面积为①a2-b2;②a(a-b)+b(a-b);③(a+b)(a-b)共3种方法正确.
故选:C.
点评 此题考查平方差公式的几何背景,掌握组合图形的拼接方法与面积的计算方法是解决问题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13.计算$\sqrt{8}$-$\sqrt{2}$的结果是( )
| A. | 6 | B. | $\sqrt{6}$ | C. | $\sqrt{2}$ | D. | 4 |
8. 如图,已知BC∥DE,则下列说法不正确的是( )
如图,已知BC∥DE,则下列说法不正确的是( )
 如图,已知BC∥DE,则下列说法不正确的是( )
如图,已知BC∥DE,则下列说法不正确的是( )| A. | 两个三角形是位似图形 | B. | 点A是两个三角形的位似中心 | ||
| C. | AE:AD是相似比 | D. | 点B与点E,点C与点D是对应位似点 |
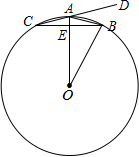 如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+