题目内容
13.关于x的方程x2-a|x|+a2-3=0有唯一的实数解,则a=±$\sqrt{3}$.分析 根据非负数的性质可知:如果方程有解,则x的值可以互为相反数,又方程有唯一的实数解,则只能x=0,由此代入求得a的数值即可.
解答 解:∵关于x的方程x2-a|x|+a2-3=0有解,
∴x的值可以互为相反数,
∵方程有唯一的实数解,
∴只能x=0,
∴a2-3=0,
解得:a=±$\sqrt{3}$.
故答案为:±$\sqrt{3}$.
点评 此题考查一元二次方程的解的意义,非负数的性质,抓住方程的解互为相反数,得出方程的唯一解为0是解决问题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.下列说法中正确的是( )
| A. | 单项式$\frac{-2{x}^{2}y}{5}$的系数是-2,次数是3 | |
| B. | -a是单项式,表示负数 | |
| C. | -6x2y+4x-1是二次三项式 | |
| D. | 单项式-$\frac{{3}^{2}ab}{2}$的次数是2,系数是-$\frac{9}{2}$ |
8. 如图,已知BC∥DE,则下列说法不正确的是( )
如图,已知BC∥DE,则下列说法不正确的是( )
 如图,已知BC∥DE,则下列说法不正确的是( )
如图,已知BC∥DE,则下列说法不正确的是( )| A. | 两个三角形是位似图形 | B. | 点A是两个三角形的位似中心 | ||
| C. | AE:AD是相似比 | D. | 点B与点E,点C与点D是对应位似点 |
5.在-1$\frac{1}{2}$,12,0,-(-5),-|-3|中,负数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.若|a-1|+(b+4)2=0,则b-a=( )
| A. | -4$\frac{1}{2}$ | B. | -2$\frac{1}{2}$ | C. | -4 | D. | -5 |
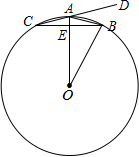 如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+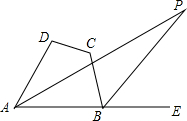 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=220°,求∠P的度数.
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=220°,求∠P的度数.