题目内容
8.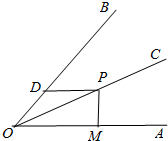 如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )
如图,OC平分∠AOB,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=3,则PD的长为( )| A. | 2 | B. | 1.5 | C. | 3 | D. | 2.5 |
分析 过点P作PN⊥OB于N,根据角平分线上的点到角的两边距离相等可得PN=PM,根据角平分线的定义求出∠AOC=30°,然后求出PM,再根据两直线平行,同位角相等可得∠PDN=60°,求出∠DPN=30°,再求解即可.
解答  解:如图,过点P作PN⊥OB于N,
解:如图,过点P作PN⊥OB于N,
∵OC平分∠AOB,PM⊥OA,
∴PN=PM,
∵OC平分∠AOB,且∠AOB=60°,
∴∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°,
∵OM=3,
∴PM=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∵PD∥OA,
∴∠PDN=∠AOB=60°,
∴∠DPN=90°-60°=30°,
∴PD=$\sqrt{3}$÷$\frac{\sqrt{3}}{2}$=2.
故选A.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,解直角三角形以及平行线的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
19.若点A(2,m)在x轴上,则点B(m-1,m+1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.
如图,梯形ABCD中,AD∥BC,AC⊥BC,且∠D=∠BAC.求证:AC2=AD•BC.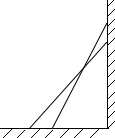 如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.
如图,一架云梯长25m,斜靠在一面墙上,梯子靠墙的一端距地面24m.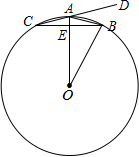 如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+ 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.