题目内容
18. 在△ABC中,AB=AC,BD=AE,∠B=∠DEC,求证:AD=CD.
在△ABC中,AB=AC,BD=AE,∠B=∠DEC,求证:AD=CD.
分析 作DF∥BC交AC于F,连接BF,由平行线的性质得出∠AFD=∠ACB,∠ADF=∠ABC,再由等腰三角形的性质和已知条件得出∠AFD=∠DEC=∠ADF,证出DE=DF,∠AED=∠BDF,由SAS证明△ADE≌△BFD,得出∠A=∠DBF,证明B、C、F、D四点共圆,由圆周角定理得出∠DBF=∠DCF,因此∠A=∠DCF,即可得出AD=CD.
解答 证明:作DF∥BC交AC于F,连接BF,如图所示: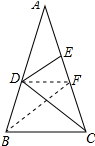
则∠AFD=∠ACB,∠ADF=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AFD=∠ABC,
∵∠B=∠DEC,
∴∠AFD=∠DEC=∠ADF,
∴DE=DF,∠AED=∠BDF,
在△ADE和△BFD中,
$\left\{\begin{array}{l}{AE=BD}&{\;}\\{∠AED=∩BDF}&{\;}\\{DE=DF}&{\;}\end{array}\right.$,
∴△ADE≌△BFD(SAS),
∴∠A=∠DBF,
∵DF∥BC,
∴∠ABC+∠BDF=180°,
∴∠ACB+∠BDF=180°,
∴B、C、F、D四点共圆,
∴∠DBF=∠DCF,
∴∠A=∠DCF,
∴AD=CD.
点评 本题考查了四点共圆、圆周角定理、全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形全等和四点共圆才能得出结论.

练习册系列答案
相关题目
9.若a,b,c是△ABC的三边长,则a2-2ab-c2+b2的值( )
| A. | 大于零 | B. | 小于零 | ||
| C. | 等于零 | D. | 与零的大小没有关系 |
10. 如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
 如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )
如图所示,某公园的一座石拱桥是圆弧形(劣弧),其跨度为12m,拱的半径为10m,则拱高为( )| A. | 3m | B. | 2m | C. | 4m | D. | $\sqrt{3}$m |
7.若抛物线y=ax2+bx+c过点(1,0),且对称轴为直线x=$\frac{1}{2}$,那么抛物线还必定经过点( )
| A. | (0,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
 已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG,求证:CD=AE.
已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG,求证:CD=AE. 如图所示,在⊙O中,弦AD∥弦BC,∠BAD=40°,求∠AOC的度数.
如图所示,在⊙O中,弦AD∥弦BC,∠BAD=40°,求∠AOC的度数.