题目内容
9．若a，b，c是△ABC的三边长，则a2-2ab-c2+b2的值（ ）| A． | 大于零 | B． | 小于零 | ||
| C． | 等于零 | D． | 与零的大小没有关系 |
分析 首先把a2-2ab-c2+b2分组分解因式，进一步利用三角形的三边关系得出答案即可．
解答 解：a2-2ab-c2+b2
=a2-2ab+b2-c2
=（a-b）2-c2
=（a-b+c）（a-b-c），
∵a，b，c是△ABC的三边长，
∴a-b+c＞0，a-b-c＜0，
∴（a-b+c）（a-b-c）＜0，
则a2-2ab-c2+b2的值小于0．
故选：B．
点评 此题考查因式分解的实际运用，掌握三角形的三边关系，完全平方公式和平方差公式是解决问题的关键．
练习册系列答案
相关题目
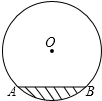如图，水平放着的圆柱形水管的截面半径是12，其中水面的高为6，求水面AB的宽度是多少？
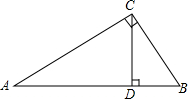如图，Rt△ABC中，CD是斜边AB上的高．求证：
在△ABC中，AB=AC，BD=AE，∠B=∠DEC，求证：AD=CD．