题目内容
13.am-2÷am•a2=1,(x2)3•x2÷x5=x3.分析 根据同底数幂的除法底数不变指数相减,可得答案;
根据幂的乘方底数不变指数相乘,可得同底数幂的乘除法,根据同底数幂的乘除法,可得答案.
解答 解:am-2÷am•a2=am-2-m+2=a0=1;
(x2)3•x2÷x5=x6•x2÷x5=x6+2-5=x3,
故答案为:1,x3.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.

练习册系列答案
相关题目
3.下列是一元一次方程的是( )
| A. | x2-3=0 | B. | 3x+y=0 | C. | 5x+4 | D. | 3-2y=0 |
3.下列说法正确的是( )
| A. | $\frac{x-2}{3}$是分式 | B. | 分式的分子为0,则分式的值为0 | ||
| C. | 将式子(a+b)÷c写成分数的形式是a+$\frac{b}{c}$ | D. | 对于任意实数,$\frac{x}{1+{x}^{2}}$总有意义 |
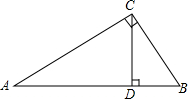 如图,Rt△ABC中,CD是斜边AB上的高.求证:
如图,Rt△ABC中,CD是斜边AB上的高.求证: 在△ABC中,AB=AC,BD=AE,∠B=∠DEC,求证:AD=CD.
在△ABC中,AB=AC,BD=AE,∠B=∠DEC,求证:AD=CD.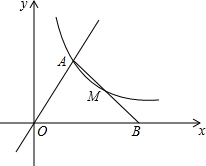 在平面直角坐标系中,已知第一象限内的点A的坐标为(1,m),OA=2,正比例函数y=$\frac{3x}{m}$和反比例函数y=$\frac{k-1}{x}$的图象都经过点A,过A作OA的垂线交x轴于点B.
在平面直角坐标系中,已知第一象限内的点A的坐标为(1,m),OA=2,正比例函数y=$\frac{3x}{m}$和反比例函数y=$\frac{k-1}{x}$的图象都经过点A,过A作OA的垂线交x轴于点B.