题目内容
 如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).(1)画出△ABC和△A1B1C1;
(2)求△A1B1C1的面积.
考点:作图-平移变换
专题:作图题
分析:(1)根据网格结构找出点A、B、C的位置,然后顺次连接即可,再根据点P、P1的坐标确定出变化规律,然后找出点A1、B1、C1的位置,然后顺次连接即可;
(2)利用三角形所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
(2)利用三角形所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
解答:解:(1)△ABC和△A1B1C1如图所示;
(2)S△A1B1C1=3×2-
×1×2-
×1×2-
×1×3
=6-1-1-1.5
=6-3.5
=2.5.

(2)S△A1B1C1=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-1-1-1.5
=6-3.5
=2.5.

点评:本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
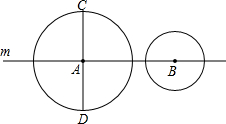 如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是
如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是