题目内容
2．在边长分别为8、15、17的三角形铁片上剪下一个最大的圆铁片，则它的半径为3．分析 由在边长分别为8、15、17的三角形铁片上剪下一个最大的圆铁片，易得此三角形是直角三角形，此圆是其内切圆，继而求得答案．
解答 解：∵82+152=172，
∴边长分别为8、15、17的三角形是直角三角形，
∴剪下一个最大的圆铁片的半径为：$\frac{8×15}{8+15+17}$=3．
故答案为：3．
点评 此题考查了三角形的内切圆的性质以及直角三角形的判定．注意判定此三角形是直角三角形是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．若ax2+bx+c＜0（a≠0）无解，则a，b，c应满足（ ）
| A． | a＞0，△≤0 | B． | a＞0，△＞0 | C． | a＜0，△＜0 | D． | a＜0，△≤0 |
在Rt△ABC中，AC=3，BC=4，∠ACB=90°．若以点C为圆心，r为半径的圆与直线AB不相离，求r的取值范围．
17．在平面直角坐标系中，已知线段AB的两个端点分别是A（4，-1），B（1，1）将线段AB平移后得到线段A′B′，若点A的坐标为（-2，2），则点B′的坐标为（ ）
| A． | （-5，4） | B． | （4，3） | C． | （-1，-2） | D． | （-2，-1） |
7．分式方程$\frac{1}{x+1}$+$\frac{1}{{x}^{2}+x}$=0去分母应乘的最简公分母是（ ）
| A． | x+1 | B． | x2 | C． | x（x+1） | D． | x（x+1）2 |
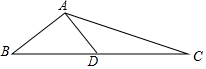如图，在△ABC中，AB=5，AC=13，边BC上的中线AD=6．
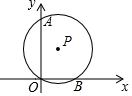如图，在直角坐标系中，⊙P的圆心坐标为（1，$\sqrt{3}$），半径为2，⊙P分别交y轴，x轴于点A，B，求证：