题目内容
19.(1)解方程:x2-2x-1=0.(2)解不等式组:$\left\{{\begin{array}{l}{x-3(x-2)≤8}\\{x-1<\frac{x+1}{3}}\end{array}}\right.$.
分析 (1)确定a、b、c的值,判断△的值,最后根据求根公式求解;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)a=1,b=-2,c=-1.
b2-4ac=(-2)2-4×1×(-1)=8
∴x=$\frac{{2±2\sqrt{2}}}{2}$
∴${x_1}=1+\sqrt{2},{x_2}=1-\sqrt{2}$.
(2)解不等式①得:x≥-1,
解不等式②得:x<2,
所以不等式组的解集为-1≤x<2.
点评 本题考查的是解一元二次方程和解一元一次不等式组得基本能力,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
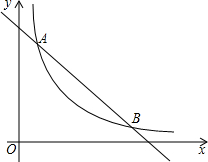 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$与一次函数y=-x+b交于点A(1,6-k),B(m,1).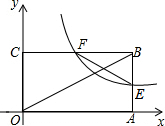 如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.
如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.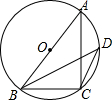 如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=$\frac{4}{5}$,则AB=$\frac{\sqrt{41}}{2}$.
如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=$\frac{4}{5}$,则AB=$\frac{\sqrt{41}}{2}$.