题目内容
9.已知△ABC∽△A1B1C1,△ABC的角平分线AM=3,△A1B1C1的角平分线A1N=1,则△ABC与△A1B1C1的面积比为9:1.分析 由△ABC∽△A1B1C1,△ABC的角平分线AM=3,△A1B1C1的角平分线A1N=1,根据相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比,即可求得其相似比,然后由相似三角形面积比等于相似比的平方,求得答案.
解答 解:∵△ABC∽△A1B1C1,△ABC的角平分线AM=3,△A1B1C1的角平分线A1N=1,
∴△ABC与△A1B1C1的相似比为3:1,
∴△ABC与△A1B1C1的面积比,9:1.
故答案为:9:1.
点评 此题考查了相似三角形的性质.注意熟记定理是解此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
4.抛物线y=-$\frac{1}{2}{x}^{2}$-3的顶点坐标是( )
| A. | ($\frac{1}{2}$,-3) | B. | (-3,0) | C. | (0,-3) | D. | (0,3) |
 如图,AB∥CD,AB=CD.AD、BC相交于点O,OE=OF,BE、CF分别交AD于点E、F.根据以上信息:
如图,AB∥CD,AB=CD.AD、BC相交于点O,OE=OF,BE、CF分别交AD于点E、F.根据以上信息: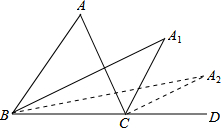 如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.
如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.