题目内容
17.已知五边形ABCDE∽五边形MNOPQ,如果AB=12,MN=6,AE=7,∠E=82°,则MQ=3.5,∠Q=82°,五边形ABCDE与五边形MNOPQ的周长之比是2:1.分析 由五边形ABCDE∽五边形MNOPQ,如果AB=12,MN=6,AE=7,∠E=82°,根据相似多边形的对应边长比例,对应角相等,即可求得MQ的长与∠Q的度数,再由相似多边形的周长比等于相似比,即可求得五边形ABCDE与五边形MNOPQ的周长之比.
解答 解:∵五边形ABCDE∽五边形MNOPQ,AB=12,MN=6,AE=7,
∴$\frac{AB}{MN}=\frac{AE}{MQ}$,
即$\frac{12}{6}=\frac{7}{MQ}$,
∴MQ=3.5;
∵∠E=82°,
∴∠Q=∠E=82°;
∵AB:MN=12:6=2:1,
∴五边形ABCDE与五边形MNOPQ的周长之比是:2:1.
故答案为:3.5,82°,2:1.
点评 此题考查了相似多边形的性质.注意相似多边形的对应边成比例,对应角相等,对应周长的比等于相似比.

练习册系列答案
相关题目
7.一件衣服按原价的八折出售,价格为a元,则这件衣服的原价为( )
| A. | $\frac{a}{80%}$元 | B. | 80%a元 | C. | 20%a元 | D. | $\frac{a}{20%}$元 |
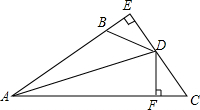 如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.
如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.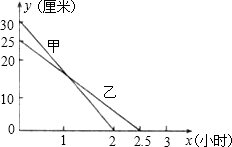 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题