题目内容
19.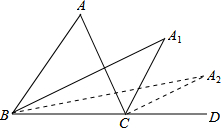 如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.
如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A1BC和∠A1CD的平分线交于点A3,则∠A3=8°.
分析 利用角平分线的性质、三角形外角性质,易证∠A1=$\frac{1}{2}$∠A,进而可求∠A1,由于∠A1=$\frac{1}{2}$∠A,∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,故∠A3=$\frac{1}{2}$∠A2=$\frac{1}{{2}^{3}}$∠A.
解答 解:∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=$\frac{1}{2}$∠ABC,∠A1CA=$\frac{1}{2}$∠ACD,
∵∠A1CD=∠A1+∠A1BC,
即$\frac{1}{2}$∠ACD=∠A1+$\frac{1}{2}$∠ABC,
∴∠A1=$\frac{1}{2}$(∠ACD-∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD-∠ABC,
∴∠A1=$\frac{1}{2}$∠A,
∴∠A1=$\frac{1}{2}$×64°=32°,
∵∠A1=$\frac{1}{2}$∠A,∠A2=$\frac{1}{2}$∠A1=$\frac{1}{{2}^{2}}$∠A,
∴∠A3=$\frac{1}{2}$∠A2=$\frac{1}{{2}^{3}}$∠A=$\frac{1}{8}$×64°=8°.
故答案为:8°.
点评 本题考查了三角形内角和定理、角平分线的性质、三角形外角的性质,解题的关键是推导出∠A1=$\frac{1}{2}$∠A,并能找出规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列说法错误的是( )
| A. | 若AP=BP,则点P是线段的中点 | B. | 若点C在线段AB上,则AB=AC+BC | ||
| C. | 顶点在圆心的角叫做圆心角 | D. | 两点之间,线段最短 |
4.下面图形是多边形的是( )
| A. |  | B. |  | C. |  | D. |  |
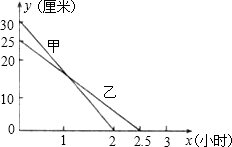 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题
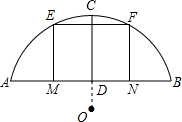 某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m.
某桥主拱桥是圆弧形,跨度AB=60m.拱高CD=10m. 在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点.
在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点.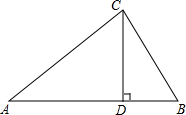 如图,在R△ABC中,∠ACB=90°,CD⊥AB,AC=5,CD=3,求BC.
如图,在R△ABC中,∠ACB=90°,CD⊥AB,AC=5,CD=3,求BC.