题目内容
5.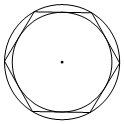 已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )| A. | $\frac{4}{3}π$ | B. | 4π | C. | 2π | D. | $\frac{{2\sqrt{3}}}{3}$π |
分析 作出正六边形的边心距,连接正六边形的一个顶点和中心可得到一直角三角形.解直角三角形即可.
解答 解:作OM⊥AB于M,如图所示:
正六边形可以分六个全等等边三角形,则这样的等边三角形的一边上的高为原正六边形的内切圆的半径;
因为等边三角形的边长为正六边形的外接圆的半径,
所以内切圆面积与外接圆面积之比=(sin60°)2=$\frac{3}{4}$,
∴正六边形的外接圆面积是$\frac{4}{3}π$.
故选A.
点评 本题利用了正六边形可以分六个全等等边三角形,则这样的等边三角形的一边上的高为原正六边形的内切圆的半径,等边三角形的边长为正六边形的外接圆的半径的性质求解.

练习册系列答案
相关题目
6.下列四个数中,其相反数是正整数的是( )
| A. | 3 | B. | -2 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
17.对于任意大于或等于4的偶数,存在下列勾股数:
(1)根据以上规律,请你直接写出第7组勾股数:
(2)请你猜想出第n组(n为正整数),并证明这是一组勾股数.
| 组别 | a | b | c |
| 第1组 | 4=2×2 | 3=22-1 | 5=22+1 |
| 第2组 | 6=2×3 | 8=32-1 | 10=32+1 |
| 第3组 | 8=2×4 | 15=42-1 | 17=42+1 |
(2)请你猜想出第n组(n为正整数),并证明这是一组勾股数.
15.如果三角形的两边分别为3和5,那么第三边可能是( )
| A. | 3 | B. | 1 | C. | 2 | D. | 8 |
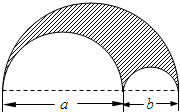 如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆
如图,一块直径为a+b的半圆形钢板,从中挖去直径分别为a与b的两个半圆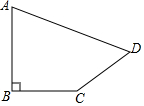 如图所示,在四边形ABCD中,∠B=90°,AB=2,BC=CD=1,AD=$\sqrt{6}$,试求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠B=90°,AB=2,BC=CD=1,AD=$\sqrt{6}$,试求四边形ABCD的面积.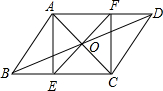 如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.
如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.