题目内容
10.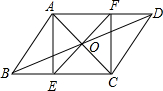 如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.
如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.
分析 首先利用平行四边形的性质得出BC∥AD,AO=CO,进而利用全等三角形的判定方法△COE≌△AOF(AAS),进而得出EO=FO,得出四边形AECF是平行四边形,再由AE⊥BC,即可得出结论.
解答 解:四边形AECF是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴BC∥AD,AO=CO,
∴∠AFO=∠CEO,
在△COE和△AOF中,$\left\{\begin{array}{l}{∠AFO=∠CEO}&{\;}\\{∠FOA=∠COE}&{\;}\\{AO=CO}&{\;}\end{array}\right.$,
∴△COE≌△AOF(AAS),
∴EO=FO,
∵AO=CO,
∴四边形AECF是平行四边形,
又∵AE⊥BC,
∴四边形AECF是矩形.
点评 此题主要考查了平行四边形的性质与判定、矩形的判定以及全等三角形的判定与性质,得出△COE≌△AOF是解题关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
5.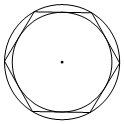 已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
 已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )| A. | $\frac{4}{3}π$ | B. | 4π | C. | 2π | D. | $\frac{{2\sqrt{3}}}{3}$π |
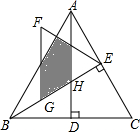 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{\sqrt{3}}{6}$.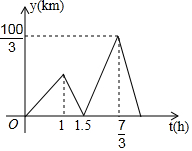 不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为55千米.
不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为55千米.