题目内容
17.对于任意大于或等于4的偶数,存在下列勾股数:| 组别 | a | b | c |
| 第1组 | 4=2×2 | 3=22-1 | 5=22+1 |
| 第2组 | 6=2×3 | 8=32-1 | 10=32+1 |
| 第3组 | 8=2×4 | 15=42-1 | 17=42+1 |
(2)请你猜想出第n组(n为正整数),并证明这是一组勾股数.
分析 (1)根据前面的几组数可以得到每组勾股数与各组的序号之间的关系,如果是第n组数,则这组数中的第一个数是2(n+1),第二个是:(n+1)2-1,第三个数是:(n+1)2+1.根据这个规律即可解答;
(2)根据勾股定理的逆定理即可求解.
解答 (1)解:观察前3组数据的规律可知:第一个数是2(n+1);第二个是:(n+1)2-1;第三个数是:(n+1)2+1.
所以第7组勾股数是16,63,65.
(2)第n组是第一个数是2(n+1);第二个是:(n+1)2-1;第三个数是:(n+1)2+1.
证明:∵[2(n+1)]2+[(n+1)2-1]2
=4(n+1)2+(n+1)4-2(n+1)2+1
=(n+1)4+2(n+1)2+1
=[(n+1)2+1]2,
故这是一组勾股数.
点评 此题考查了勾股数,观察已知的几组数的规律,是解决本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.下列运算正确的是( )
| A. | x2+x3=x5 | B. | (x-2)2=x2-4 | C. | (x3)4=x7 | D. | 2x2?x3=2x5 |
5.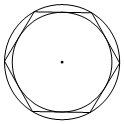 已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
 已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )
已知一个正六边形的内切圆面积是π,则它的外接圆面积是( )| A. | $\frac{4}{3}π$ | B. | 4π | C. | 2π | D. | $\frac{{2\sqrt{3}}}{3}$π |
7. 如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
 如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )
如图,已知点O是直线AB上一点,∠1=65°,则∠2的度数( )| A. | 25° | B. | 65° | C. | 105° | D. | 115° |
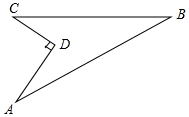 如图,已知AD=4,CD=3,BC=12,AB=13,∠ADC=90°,求四边形ABCD的面积.
如图,已知AD=4,CD=3,BC=12,AB=13,∠ADC=90°,求四边形ABCD的面积.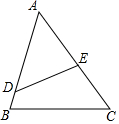 如图,∠ADE=∠C,AD=CE=2,AE=1,求$\frac{DE}{BC}$的值.
如图,∠ADE=∠C,AD=CE=2,AE=1,求$\frac{DE}{BC}$的值.