题目内容
7.用加减法解方程组:(1)$\left\{\begin{array}{l}{2x+y=8}\\{x-y=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+3y=-1}\\{3x-2y=8}\end{array}\right.$
(3)$\left\{\begin{array}{l}{4x-3y=11}\\{2x+y=13}\end{array}\right.$
(4)$\left\{\begin{array}{l}{x+y=3}\\{5x-3(x+y)=1}\end{array}\right.$.
分析 (1)利用加减法即可求解;
(2)把x的系数化成相等,然后两式相减求得y,则x即可求得;
(3)利用加减法即可求解;
(4)首先把方程组中的第二个方程化简成一般形式,然后利用加减法即可求解.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=-8…①}\\{x-y=-1…②}\end{array}\right.$,
①+②得3x=-9,
解得x=-3,
把x=-3代入方程②得-3-y=-1,
解得y=-2,
则方程组的解是$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{x+3y=-1…①}\\{3x-2y=8…②}\end{array}\right.$,
①×3-②得11y=-11,
解得y=-1,
把y=-1代入①得x-3=-1,
解得x=2,
则方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{4x-3y=11…①}\\{2x+y=13…②}\end{array}\right.$,
①+②×3得10x=50,
解得x=5,
把x=5代入②得10+y=13,
解得y=3,
则方程组的解是$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{x+y=3…①}\\{5x-3(x+y)=1…②}\end{array}\right.$,
整理②得2x-3y=1…③,
①×2-③得5y=5,
解得y=1,
把y=1代入①得x+1=3,
解得x=2,
则方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查二元一次方程组的解法,解方程组的基本思想是消元、消元的方法有代入消元法和加减消元法两种.

| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
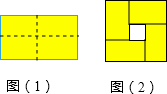 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A. | 2ab | B. | (a+b)2 | C. | (a-b)2 | D. | a2-b2 |
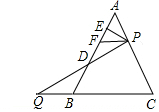 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.