题目内容
19. 如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?
如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?
分析 根据两直线平行,同位角相等求出∠EAD=∠B,再根据角平分线的定义可得∠DAC=∠EAD,然后利用两直线平行,内错角相等可得∠C=∠DAC.
解答 解:∵AD∥BC,∠B=64°,
∴∠EAD=∠B=64°,
∵AD是∠EAC的平分线,
∴∠DAC=∠EAD=64°,
又∵AD∥BC,
∴∠C=∠DAC=64°.
点评 本题主要考查了平行线的性质,角平分线的定义的运用,熟记平行线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:
(1)根据上表填空;
①方程ax2+bx+c=0的两个根分别是x1=-2和x2=1.
②抛物线经过点(-3,8);
③在对称轴左侧,y随x增大而减小;
(2)求抛物线y=ax2+bx+c的解析式.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | -4 | 0 | 8 |
①方程ax2+bx+c=0的两个根分别是x1=-2和x2=1.
②抛物线经过点(-3,8);
③在对称轴左侧,y随x增大而减小;
(2)求抛物线y=ax2+bx+c的解析式.
10.下列各组数据不能作为直角三角形的三边长的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 13,16,18 |
4.化简$\sqrt{27}+\sqrt{48}$的结果是( )
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
 如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.
如图,在△ABC中,AB=AC,∠A=40°,点D在AC上,BD=BC,求∠ABD的度数.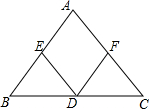 如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.
如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数. 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|. 如图,已知AB∥CD,∠1=∠2,那么AE平行于DF吗?请说明理由.
如图,已知AB∥CD,∠1=∠2,那么AE平行于DF吗?请说明理由.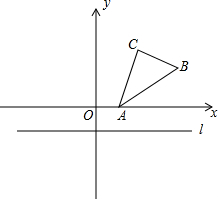 在平面直角坐标系中,已知点A(1,0),B(4,2),C(2,3).
在平面直角坐标系中,已知点A(1,0),B(4,2),C(2,3).