题目内容
9.抛物线y=ax2+bx+c上,部分点的横、纵坐标x、y的对应值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | -4 | 0 | 8 |
①方程ax2+bx+c=0的两个根分别是x1=-2和x2=1.
②抛物线经过点(-3,8);
③在对称轴左侧,y随x增大而减小;
(2)求抛物线y=ax2+bx+c的解析式.
分析 (1)①观察表格中y=0时x的值,即可确定出所求方程的解;
②利用对称性确定出x=-3时y的值,确定出所求点坐标即可;
③利用二次函数增减性确定出结果即可;
(2)利用待定系数法确定出抛物线解析式即可.
解答 解:(1)①观察表格得:方程ax2+bx+c=0的两个根分别是x1=-2和x2=1;
②抛物线经过点(-3,8);
③在对称轴左侧,y随x的增大而减小;
故答案为:①x1=-2,x2=1;②8;③减小;
(2)设抛物线解析式为y=ax2+bx+c,
把(-2,0),(1,0)、(0,-4)代入得:$\left\{\begin{array}{l}{4a-2b+c=0}\\{a+b+c=0}\\{c=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=2}\\{c=-4}\end{array}\right.$,
则抛物线解析式为y=2x2+2x-4.
点评 此题考查了抛物线与x轴的交点,以及待定系数法求二次函数解析式,熟练掌握二次函数的图象与性质是解本题的关键.

练习册系列答案
相关题目
18. 如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
 如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=40°,以C为圆心,CB的长为半径画弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.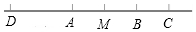 已知线段AB=20cm,点M是线段AB的中点,点C是AB延长线上一点,AC=3BC,点D是线段BA延长线上一点,AD=AB.
已知线段AB=20cm,点M是线段AB的中点,点C是AB延长线上一点,AC=3BC,点D是线段BA延长线上一点,AD=AB. 如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?
如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?