题目内容
14.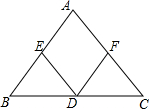 如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.
如图,D、E、F分别是BC、AB、AC的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.
分析 根据平行线的性质:两直线平行,同旁内角互补,以及同角的补角相等,进行计算即可.
解答 解:∵DE∥AC( 已知 ),
∴∠A+∠AED=180°(两直线平行,同旁内角互补),
∵DF∥AB( 已知 ),
∴∠AED+∠FDE=180°(两直线平行,同旁内角互补),
∴∠A=∠FDE=70°(同角的补角相等).
点评 本题主要考查了平行线的性质以及同角的补角相等的运用,解答本题的关键是掌握:两直线平行,同旁内角互补.

练习册系列答案
相关题目
5.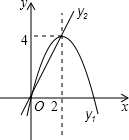 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1=y2,记M=y1=y2,下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有( )| A. | ③④ | B. | ②③ | C. | ②④ | D. | ①④ |
6.矩形具有而菱形不具有的性质是( )
| A. | 两组对边分别平行 | B. | 对角线相等 | ||
| C. | 对角线互相平行 | D. | 对角线互相垂直 |
4.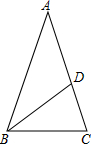 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )| A. | 30° | B. | 40° | C. | 36° | D. | 45° |
 如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.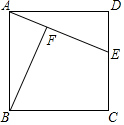 如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F.
如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F. 如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?
如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?