题目内容
11. 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.
分析 先根据数轴判断a+1<0,b-1>0,a-b<0,然后再根据二次根式的性质化简原式即可.
解答 解:∵a<-1,b>1,a<b
∴a+1<0,b-1>0,a-b<0,
∴原式=|a+1|+|b-1|-|a-b|
=-(a+1)+(b-1)+(a-b)
=-a-1+b-1+a-b
=-2
点评 本题考查考查二次根式的性质,解题的关键是根据数轴判断:a+1<0,b-1>0,a-b<0,本题属于基础题型.

练习册系列答案
相关题目
6.矩形具有而菱形不具有的性质是( )
| A. | 两组对边分别平行 | B. | 对角线相等 | ||
| C. | 对角线互相平行 | D. | 对角线互相垂直 |
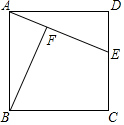 如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F.
如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F. 如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗?
如图,AD是∠EAC的平分线,AD∥BC,∠B=64°,你能算出∠EAD,∠DAC,∠C的度数吗? 在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:
在2016年宝应以“不忘初心,继续前进”为主题的青年千人毅行中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据: