题目内容
12.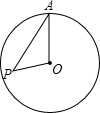 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2$\sqrt{3}$ |
分析 当PA⊥OP时,PA取最小值,∠OAP取得最大值,然后在直角三角形OPA中利用勾股定理求PA的值即可.
解答 解:在△OPA中,当∠OAP取最大值时,OP取最大值,
∴PA取最小值,
又∵OA、OP是定值,
∴PA⊥OP时,PA取最小值;
在直角三角形OPA中,OA=3,OP=$\sqrt{3}$,
∴PA=$\sqrt{9-3}$=$\sqrt{6}$.
故选B.
点评 本题考查了解直角三角形.解答此题的关键是找出“当PA⊥OP时,PA取最小值”即“PA⊥OP时,∠OAP取最大值”这一隐含条件.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
12.以等腰三角形底角的度数x(单位:度)为自变量,顶角的度数y为因变量的函数关系式为( )
| A. | y=180-2x(0<x<90) | B. | y=180-2x(0<x≤90) | C. | y=180-2x(0≤x<90) | D. | y=180-2x(0≤x≤90) |
17.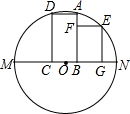 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 12 | C. | 15 | D. | $\frac{27}{2}$ |
 如图,
如图,
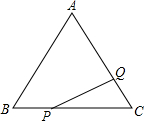 如图,等边三角形ABC的边长为6cm,点P自点B出发,以1cm/s的速度向终点C运动;点Q自点C出发,以1cm/s的速度向终点A运动.若P,Q两点分别同时从B,C两点出发,问经过多少时间△PCQ的面积是2$\sqrt{3}$cm2?
如图,等边三角形ABC的边长为6cm,点P自点B出发,以1cm/s的速度向终点C运动;点Q自点C出发,以1cm/s的速度向终点A运动.若P,Q两点分别同时从B,C两点出发,问经过多少时间△PCQ的面积是2$\sqrt{3}$cm2? 如图,用8块相同的长方形拼成一个宽为48厘米的大长方形,则每块小长方形的长和宽分别是33厘米和15厘米.
如图,用8块相同的长方形拼成一个宽为48厘米的大长方形,则每块小长方形的长和宽分别是33厘米和15厘米.