题目内容
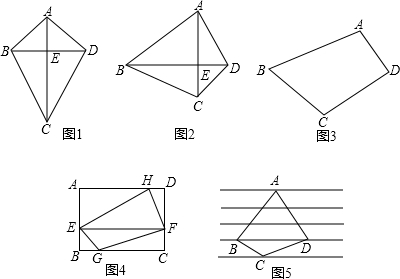
7.【写在前面】我们知道菱形的面积不仅可以用底乘以高来求,而且知道菱形的面积等于对角线乘积的一半.那么我们日常生活中常见的风筝的形状即“筝形”是不是也可以用这种方法求面积呢?如图1,四边形ABCD是我们常见的风筝的图案,其中对角线BD长为20cm,AC长为40cm,AC垂直平分BD,垂足为E,求筝形ABCD的面积.解析:由已知:S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$×BD×AE+$\frac{1}{2}$×BD×CE
=$\frac{1}{2}$×BD×(AE+CE)=$\frac{1}{2}$×BD×AC.我们发现这个结论对于筝形依然成立.
【类比总结】
满足什么条件的图形可以通过这种方法求面积呢?让我们先研究下面图形的面积:
如图2,四边形ABCD的对角线AC、BD互相垂直,其中对角线BD长为20cm,AC长为15cm,垂足为E,求四边形ABCD的面积.(请写出求解过程)
研究到这里,我们可以得出一个结论:
结论1:对角线互相垂直的四边形的面积等于两对角线积的一半.
【拓展提高】
通过结论1的研究对于普通的对角线不垂直的四边形的面积的求解能不能有什么启示呢?下面让我们一起来研究.
如图3所示四边形ABCD的对角线BD长为20cm,点A到BD的距离与点C到BD的距离之和为15cm,求四边形ABCD的面积.(请写出求解过程)
结论2:任意四边形的面积等于一条对角线和另一条对角线的两个端点到这条对角线的距离之和积的一半.
【小试牛刀】
(1)如图4,矩形ABCD中,AD=6cm,AB=4cm,EF∥AD,点G、H分别是AD、BC上任一点,则四边形EGFH的面积等于12cm2.
(2)如图5,四边形ABCD放在了一组平行线中,已知BD=6cm,四边形ABCD的面积为24cm2,则两条平行线间的距离为2cm.
分析 根据求出的结果得出结论即可;根据三角形的面积公式即可得出答案;
(1)过H作HM⊥EF于M,过G作GN⊥EF于N,求AB=HM+GN,根据三角形的面积公式求出即可;
(2)过A作AM⊥BD于M,过C作CN⊥BD于N,根据三角形的面积求出AM+CN,即可得出答案.
解答 解:结论1:对角线互相垂直的四边形的面积等于两对角线积的一半,
如图3,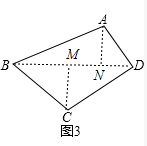
连接BD,过A作AN⊥BD于N,过C作CM⊥BD于M,
S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD×AN+$\frac{1}{2}$BD×CM
=$\frac{1}{2}$BD×(AN+CM)
=$\frac{1}{2}$×20cm×15cm
=150cm2,
即任意四边形的面积等于一条对角线和另一条对角线的两个端点的距离之和积的一半,
故答案为:两对角线积的一半,一条对角线和另一条对角线的两个端点的距离之和积的一半;
(1)如图4,过H作HM⊥EF于M,过G作GN⊥EF于N,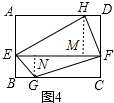
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,AB=DC,∠A=∠B=90°,
∵EF∥AD,
∴四边形AEFD是平行四边形,EF∥BC,
∴EF=AD=6cm,
∵HM⊥EF,
∴∠AEF=∠HMF=90°,
∴AE∥HM,
∵AH∥EM,∠A=90°,
∴四边形AEMH是矩形,
∴AE=HM,
同理BE=GN,
∴HM+GN=AB=4cm,
∴S四边形EGFH=S△HEF+S△GEF
=$\frac{1}{2}$EF×HM+$\frac{1}{2}$EF×GN
=$\frac{1}{2}$EF×(HM+GN)
=$\frac{1}{2}$EF×AB
=$\frac{1}{2}$×6cm×4cm
=12cm2,
故答案为:12;
(2)如图5,过A作AM⊥BD于M,过C作CN⊥BD于N,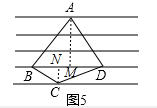
S四边形ABCD=S△ABD+S△CBD
=$\frac{1}{2}$BD×AM+$\frac{1}{2}$BD×CN
=$\frac{1}{2}$BD×(AM+CN),
即$\frac{1}{2}$×6cm×(AM+CN)=24cm2,
解得:AM+CN=8cm,
即两条平行线间的距离为2cm.
故答案为:2.
点评 本题考查了三角形的面积,矩形的性质和判定的应用,把求不规则图形的面积转化成求规则图形的面积是解此题的关键,此题是一道中档题目,难度适中.

| A. | 4 | B. | 20072 | C. | 22007 | D. | 42007 |
| A. | $\sqrt{8}$-$\sqrt{2}$=2 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b |
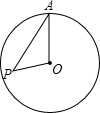 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2$\sqrt{3}$ |
 如图,已知正方形ABCD面积等于9cm2,正方形DEFG的面积等于4cm2,求阴影部分的面积S.
如图,已知正方形ABCD面积等于9cm2,正方形DEFG的面积等于4cm2,求阴影部分的面积S.