题目内容
15. 如图,
如图,若∠A=∠3,则AD∥BE;
若∠2=∠E,则BD∥CE;
若∠A+∠ABE=180°,则AD∥BE.
分析 根据平行线的判定定理进行逐一解答即可.
解答 解:∵∠A=∠3,
∴AD∥BE;
∵∠2=∠E,
∴BD∥CE;
∵∠A+∠ABE=180°,
∴AD∥BE.
故答案为:AD,BE;BD,CE;A,ABE,AD,BE.
点评 本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
5.下列各组二次根式化成最简二次根式后的被开方数完全相同的是( )
| A. | $\sqrt{ab}$与$\sqrt{a{b}^{2}}$ | B. | $\sqrt{mn}$与$\sqrt{\frac{1}{m}+\frac{1}{n}}$ | ||
| C. | $\sqrt{{m}^{2}+{n}^{2}}$与$\sqrt{{m}^{2}-{n}^{2}}$ | D. | $\sqrt{\frac{8}{9}{a}^{3}{b}^{2}}$与$\sqrt{\frac{9}{2}{a}^{3}{b}^{4}}$ |
6.方程$\frac{2x}{{x}^{2}-4}$-$\frac{2}{x-2}$=$\frac{1}{x+2}$的解是( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 无解 |
7.下列各式中,运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=2 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b |
12.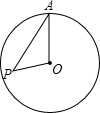 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2$\sqrt{3}$ |
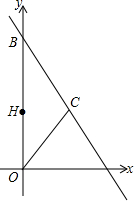 如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根.
如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根. 如图,已知正方形ABCD面积等于9cm2,正方形DEFG的面积等于4cm2,求阴影部分的面积S.
如图,已知正方形ABCD面积等于9cm2,正方形DEFG的面积等于4cm2,求阴影部分的面积S.