题目内容
4．
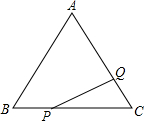如图，等边三角形ABC的边长为6cm，点P自点B出发，以1cm/s的速度向终点C运动；点Q自点C出发，以1cm/s的速度向终点A运动．若P，Q两点分别同时从B，C两点出发，问经过多少时间△PCQ的面积是2$\sqrt{3}$cm2？
分析 首先设经过xs△PCQ的面积是2$\sqrt{3}$cm2，则PC=6-x，△PCQ的高是CQ•sin60°=$\frac{\sqrt{3}}{2}$x，由此列出方程解答即可．
解答 解：设经过xs△PCQ的面积是2$\sqrt{3}$cm2，由题意得
$\frac{1}{2}$（6-x）$\frac{\sqrt{3}}{2}$x=2$\sqrt{3}$
解得：x1=2，x2=4，
答：经过2s或4s△PCQ的面积是2$\sqrt{3}$cm2．
点评 此题考查一元二次方程的实际运用，利用特殊角的三角函数，以及等边三角形的性质求得底和高是解决问题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
6．方程$\frac{2x}{{x}^{2}-4}$-$\frac{2}{x-2}$=$\frac{1}{x+2}$的解是（ ）
| A． | -2 | B． | 2或-2 | C． | 2 | D． | 无解 |
7．下列各式中，运算正确的是（ ）
| A． | $\sqrt{8}$-$\sqrt{2}$=2 | B． | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C． | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D． | $\sqrt{{a}^{2}+{b}^{2}}$=a+b |
12．
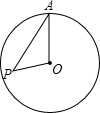如图，点P在半径为3的⊙O内，OP=$\sqrt{3}$，A为⊙O上一点，当∠OAP取最大值时，PA的长等于（ ）
如图，点P在半径为3的⊙O内，OP=$\sqrt{3}$，A为⊙O上一点，当∠OAP取最大值时，PA的长等于（ ）| A． | $\frac{3}{2}$ | B． | $\sqrt{6}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 2$\sqrt{3}$ |
9．某工程甲独做12天完成，乙独做8天完成，现在由甲先做3天，乙再参加合做．设完成此工程一共用了x天，则下列方程正确的是（ ）
| A． | $\frac{x+3}{12}$+$\frac{x}{8}$=1 | B． | $\frac{x}{12}$+$\frac{x-3}{8}$=1 | C． | $\frac{x}{12}$+$\frac{x}{8}$=1 | D． | $\frac{x+3}{12}$+$\frac{x-3}{8}$=1 |