题目内容
17.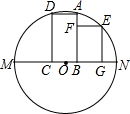 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 12 | C. | 15 | D. | $\frac{27}{2}$ |
分析 连接OA,OE,根据矩形ABCD中,AB=2AD可知点O是BC的中点,设OB=x,⊙O的半径为r,则AB=4x,根据勾股定理列出x,r的关系式,同理,在Rt△OEG中列出关于x,r的关系式,两式联立求出x的值,进而可得出结论.
解答 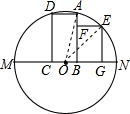 解:连接OA,OE,
解:连接OA,OE,
∵矩形ABCD中,AB=2AD,
∴点O是BC的中点,
设OB=x,⊙O的半径为r,则AB=4x,
∵AB2+OB2=OA2,即(4x)2+x2=r2①.
∵GE=2BG=4,
∴BG=2.
在Rt△OEG中,
∵EG2+OG2=OE2,即42+(2+x)2=r2②,
①②联立得,x=$\frac{5}{4}$,
∴BC=2x=$\frac{5}{2}$,AB=4x=5,
∴矩形ABCD的面积=$\frac{5}{2}$×5=$\frac{25}{2}$.
故选A.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
12.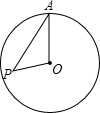 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2$\sqrt{3}$ |
9.某工程甲独做12天完成,乙独做8天完成,现在由甲先做3天,乙再参加合做.设完成此工程一共用了x天,则下列方程正确的是( )
| A. | $\frac{x+3}{12}$+$\frac{x}{8}$=1 | B. | $\frac{x}{12}$+$\frac{x-3}{8}$=1 | C. | $\frac{x}{12}$+$\frac{x}{8}$=1 | D. | $\frac{x+3}{12}$+$\frac{x-3}{8}$=1 |
 如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.
如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.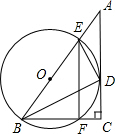 如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.
如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.