题目内容
14.分解因式:2x2+4x+2=2(x+1)2.分析 根据提公因式,可得完全平方公式,根据完全平方公式,可得答案.
解答 解:原式=2(x2+2x+1)=2(x+1)2,
故答案为:2(x+1)2.
点评 本题考查了因式分解,先提取公因式2,再利用和的平方公式.

练习册系列答案
相关题目
5.下列各组二次根式化成最简二次根式后的被开方数完全相同的是( )
| A. | $\sqrt{ab}$与$\sqrt{a{b}^{2}}$ | B. | $\sqrt{mn}$与$\sqrt{\frac{1}{m}+\frac{1}{n}}$ | ||
| C. | $\sqrt{{m}^{2}+{n}^{2}}$与$\sqrt{{m}^{2}-{n}^{2}}$ | D. | $\sqrt{\frac{8}{9}{a}^{3}{b}^{2}}$与$\sqrt{\frac{9}{2}{a}^{3}{b}^{4}}$ |
9.若x+y=2,x2+y2=4,则x2007+y2007的值是( )
| A. | 4 | B. | 20072 | C. | 22007 | D. | 42007 |
6.方程$\frac{2x}{{x}^{2}-4}$-$\frac{2}{x-2}$=$\frac{1}{x+2}$的解是( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 无解 |
12.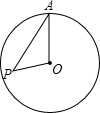 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,A为⊙O上一点,当∠OAP取最大值时,PA的长等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2$\sqrt{3}$ |
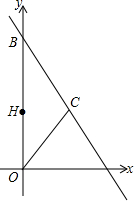 如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根.
如图,在平面直角坐标系中,直线AB交x轴的正半轴于点A,交y轴正半轴于点B,点C在直线AB上,OC=OA,且OA、OB的长(OB>OA)是方程x2-15x+50=0的根.