题目内容
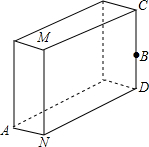如图所示：一块砖宽AN=3cm，长ND=9cm，CD上的点B距地面的高BD=5cm，地面上A处的一只蚂蚁要到B点觅食，则需要爬行的最短路程为多少？考点：平面展开-最短路径问题
专题：
分析：要求不在同一平面内的两点间的最短距离，首先要把两点所在的两个平面展开到一个平面内，然后根据题意确定数据，再根据勾股定理即可求解．
解答：
解：如图所示，连接AB，则AB的长即为A处到B处的最短路程．
在Rt△ABD中，
∵AD=AN+ND=3+9=12，BD=5，
∴AB=
=13cm．
答：需要爬行的最短路程为13cm．
解：如图所示，连接AB，则AB的长即为A处到B处的最短路程．在Rt△ABD中，
∵AD=AN+ND=3+9=12，BD=5，
∴AB=
| (3+9)2+52 |
答：需要爬行的最短路程为13cm．
点评：本题的是平面展开-最短路径问题，解答此类问题时要先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题
练习册系列答案
快捷英语周周练系列答案
相关题目
如图，⊙O是△ABC的内切圆，若∠ABC=60°，∠ACB=40°，则∠BOC=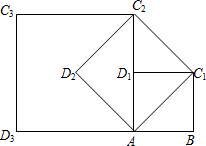
如图，在正方形ABC1D1中，AB=1．连接AC1，以AC1为边作第二个正方形AC1C2D2；连接AC2，以AC2为边作第三个正方形AC2C3D3．则已知关于x的分式方程
=1，下列说法中正确的是（ ）
| 2m |
| x+6 |
| A、该方程的解是x=2m-6 |
| B、m＜3时，该方程的解为负数 |
| C、m＞3时，该方程的解为正数 |
| D、m≠3时，该方程无解 |
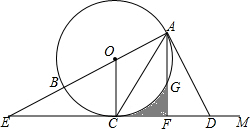如图，AB是⊙O的直径，CM是⊙O的切线，切点为C，延长AB交CD于点E，连接AC，在射线CM上取一点D使DA=DC，作AF⊥ED于点F，交⊙O于点G，
如图，已知A（-4，n）、B（2，-4）是一次函数y=k1x+b1的图象和反比例函数y=已知⊙O1的半径为1，⊙O2的半径为5，若⊙O1和⊙O2有2个公共点，则圆心距O1O2的长度可以是（ ）
| A、4 | B、5 | C、6 | D、9 |