题目内容
已知⊙O1的半径为1,⊙O2的半径为5,若⊙O1和⊙O2有2个公共点,则圆心距O1O2的长度可以是( )
| A、4 | B、5 | C、6 | D、9 |
考点:圆与圆的位置关系
专题:
分析:根据公共点的个数得到⊙O1和⊙O2相交,则根据圆与圆的位置关系得到4<O1O2<6,然后对各选项进行判断.
解答:解:∵⊙O1和⊙O2有2个公共点,
∴⊙O1和⊙O2相交,
∴4<O1O2<6.
故选B.
∴⊙O1和⊙O2相交,
∴4<O1O2<6.
故选B.
点评:本题考查了圆和圆的位置关系:两圆的圆心距为d、两圆的半径分别为R,r,则两圆外离?d>R+r;两圆外切?d=R+r;两圆相交?R-r<d<R+r(R≥r);两圆内切?d=R-r(R>r);两圆内含?d<R-r(R>r).

练习册系列答案
相关题目
袋中有4个除颜色外其余都相同的小球,其中1个红色,1个黑色,2个白色.现随机从袋中摸取两个球,则摸出的球都是白色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
本学期的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为1.3、0.4,由此可知( )
| A、甲比乙的成绩稳定 |
| B、乙比甲的成绩稳定 |
| C、甲乙两人的成绩一样稳定 |
| D、无法确定谁的成绩更稳定 |
函数y=kx-k与y=kx2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
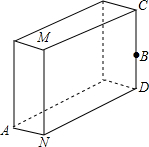 如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?
如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少? 如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长.
如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长. 在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.
在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.