题目内容
 如图,⊙O是△ABC的内切圆,若∠ABC=60°,∠ACB=40°,则∠BOC=
如图,⊙O是△ABC的内切圆,若∠ABC=60°,∠ACB=40°,则∠BOC=考点:三角形的内切圆与内心
专题:计算题
分析:根据三角形内心的性质得到OB平分∠ABC,OC平分∠ACB,根据角平分线定义得∠OBC=
∠ABC=30°,∠OCB=
∠ACB=20°,然后根据三角形内角和定理计算∠BOC.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵⊙O是△ABC的内切圆,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC=30°,∠OCB=
∠ACB=20°,
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-20°=130°.
故答案为130.
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠OBC-∠OCB=180°-30°-20°=130°.
故答案为130.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.
如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC的中点.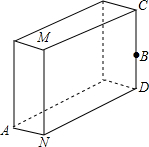 如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?
如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少? 先填空,后作图:
先填空,后作图: