题目内容
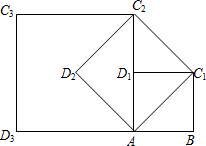 如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则
如图,在正方形ABC1D1中,AB=1.连接AC1,以AC1为边作第二个正方形AC1C2D2;连接AC2,以AC2为边作第三个正方形AC2C3D3.则(1)第三个正方形AC2C3D3的边长为
(2)按此规律所作的第7个正方形的面积为
考点:正方形的性质
专题:规律型
分析:(1)根据正方形的对角线等于边长的
倍依次求解即可;
(2)根据(1)的计算,然后利用规律求出第7个正方形的边长,再根据正方形的面积计算即可得解.
| 2 |
(2)根据(1)的计算,然后利用规律求出第7个正方形的边长,再根据正方形的面积计算即可得解.
解答:解:(1)∵在正方形ABC1D1中,AB=1,
∴AC1=
AB=
,
第三个正方形AC2C3D3的边长=
AC1=
•
=(
)2=2;
(2)以此类推,第四个正方形的边长=(
)3=2
,
…,
第7个正方形的边长=(
)6=8,
所以,第7个正方形的面积=82=64.
故答案为:2;64.
∴AC1=
| 2 |
| 2 |
第三个正方形AC2C3D3的边长=
| 2 |
| 2 |
| 2 |
| 2 |
(2)以此类推,第四个正方形的边长=(
| 2 |
| 2 |
…,
第7个正方形的边长=(
| 2 |
所以,第7个正方形的面积=82=64.
故答案为:2;64.
点评:本题正方形的性质,主要利用了正方形的对角线等于边长的
倍,熟记性质并求出前后两个正方形的边长的关系是解题的关键.
| 2 |

练习册系列答案
相关题目
下列方程式中,有解的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,⊙O是△ABC的外接圆,若∠B=30°,AC=
如图,⊙O是△ABC的外接圆,若∠B=30°,AC=| 3 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
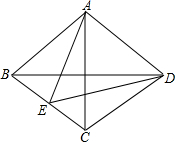 如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )
如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )| A、70° | B、60° |
| C、55° | D、50° |
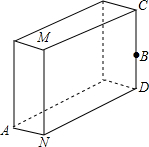 如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?
如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?