题目内容
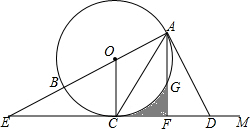 如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G,
如图,AB是⊙O的直径,CM是⊙O的切线,切点为C,延长AB交CD于点E,连接AC,在射线CM上取一点D使DA=DC,作AF⊥ED于点F,交⊙O于点G,(1)求证:AD是⊙O的切线;
(2)如果⊙O的半径是4cm,EC=4
| 3 |
考点:切线的判定与性质,扇形面积的计算
专题:
分析:(1)连接OC.欲证AD是⊙O的切线,只需证明OA⊥AD即可;
(2)连接OG.在Rt△CEO中利用正切函数求得∠E=30°,从而求得∠EOC=60°;然后由圆周角定理求得∠OAC=30°,从而求得∠ACD=60°,得出△ACD是等边三角形,根据题意证得OC∥AF,得出∠OAG=60°,进一步证得△AOG是等边三角形,进而求得∠COG=60°,根据直角三角形的性质求得OE=2OC=8,进而得出EA=12,从而求得AF=6,EF=6
最后根据S阴影=S△AEF-S△OEC-S△AOG-S扇形COG即可求得.
(2)连接OG.在Rt△CEO中利用正切函数求得∠E=30°,从而求得∠EOC=60°;然后由圆周角定理求得∠OAC=30°,从而求得∠ACD=60°,得出△ACD是等边三角形,根据题意证得OC∥AF,得出∠OAG=60°,进一步证得△AOG是等边三角形,进而求得∠COG=60°,根据直角三角形的性质求得OE=2OC=8,进而得出EA=12,从而求得AF=6,EF=6
| 3 |
解答:(1)证明:∵CM是⊙O的切线,
∴∠OCD=90°.
∴∠OCA+∠ACD=90°.
∵OA=OC,
∴∠OCA=∠OAC.
∵DA=DC,
∴∠DAC=∠ACD,
∵∠OCA+∠DAC=90°
∴∠0AC+∠CAD=90°.
∴∠OAD=90°.
∴AD是⊙O的切线.
(2)解:连接OG;
∵OC=4cm,EC=4
cm,
∴在Rt△CEO中,tanE=
=
,
∴∠E=30°.
∴∠EOC=60°,OE=2OC=8,
∴∠AOC=120°,AE=OE+OA=12,
∴AF=
AE=6,
∴EF=
=6
,
∵OA=OC,∠AOC=120°,
∴∠OAC=∠OCA=30°,
∴∠ACD=60°,
∵DA=DC,
∴△ACD是等边三角形,
∵AF⊥ED,OC⊥ED,
∴OC∥AF,
∴∠EAF=60°,
∵OA=OG,
∴△AOG是等边三角形,
∴∠AOG=60°,
∴∠COG=60°,
∴S阴影=S△AEF-S△OEC-S△AOG-S扇形COG=
EF•AF-
EC•OC-
OA•
OA-
=
×6
×6-
×4
×4-
×4×
×4-
=6
-
π.
∴∠OCD=90°.
∴∠OCA+∠ACD=90°.

∵OA=OC,
∴∠OCA=∠OAC.
∵DA=DC,
∴∠DAC=∠ACD,
∵∠OCA+∠DAC=90°
∴∠0AC+∠CAD=90°.
∴∠OAD=90°.
∴AD是⊙O的切线.
(2)解:连接OG;
∵OC=4cm,EC=4
| 3 |
∴在Rt△CEO中,tanE=
| OC |
| EC |
| ||
| 3 |
∴∠E=30°.
∴∠EOC=60°,OE=2OC=8,
∴∠AOC=120°,AE=OE+OA=12,
∴AF=
| 1 |
| 2 |
∴EF=
| AE2-AF2 |
| 3 |
∵OA=OC,∠AOC=120°,
∴∠OAC=∠OCA=30°,
∴∠ACD=60°,
∵DA=DC,
∴△ACD是等边三角形,
∵AF⊥ED,OC⊥ED,
∴OC∥AF,
∴∠EAF=60°,
∵OA=OG,
∴△AOG是等边三角形,
∴∠AOG=60°,
∴∠COG=60°,
∴S阴影=S△AEF-S△OEC-S△AOG-S扇形COG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 60π•OA2 |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 60π×42 |
| 360 |
| 3 |
| 8 |
| 3 |
点评:本题综合考查了圆周角定理、切线的判定与性质以及勾股定理的应用.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
2014年6月18日中商网报道,一种重量为0.000106千克,机身由碳纤维制成,且只有昆虫大小的机器人是全球最小的无人机,0.000106用科学记数法可表示为( )
| A、1.06×10-4 |
| B、1.06×10-5 |
| C、10.6×10-5 |
| D、106×10-6 |
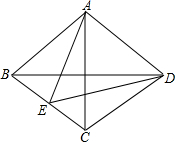 如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )
如图,在菱形ABCD中,点E在BC上,若∠ABC=∠EAD=70°,则∠CED的度数是( )| A、70° | B、60° |
| C、55° | D、50° |
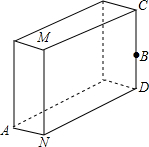 如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?
如图所示:一块砖宽AN=3cm,长ND=9cm,CD上的点B距地面的高BD=5cm,地面上A处的一只蚂蚁要到B点觅食,则需要爬行的最短路程为多少?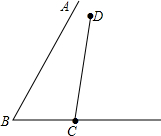 先填空,后作图:
先填空,后作图: 如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长.
如图,在△ABC中,AD、AE分别是边BC上的中线和高,AE=2cm,S△ABD=3cm2,求BC和DC的长. 在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.
在四边形ABCD中,对角线AC与BD交于点O,△ABO≌△CDO.